4894 - 机器人走路题解

题目

4894 - 机器人走路

描述

这是一个简单的生存游戏，你控制一个机器人从一个棋盘的起始点(1,1)走到棋盘的终点(n,m)。游戏的规则描述如下：
1.机器人一开始在棋盘的起始点并有起始点所标有的能量。
2.机器人只能向右或者向下走，并且每走一步消耗一单位能量。
3.机器人不能在原地停留。
4.当机器人选择了一条可行路径后，当他走到这条路径的终点时，他将只有终点所标记的能量。

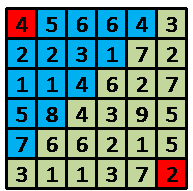
如上图，机器人一开始在(1,1)点，并拥有4单位能量，蓝色方块表示他所能到达的点，如果他在这次路径选择中选择的终点是(2,4)点，当他到达(2,4)点时将拥有1单位的能量，并开始下一次路径选择，直到到达(6,6)点。
我们的问题是机器人有多少种方式从起点走到终点。这可能是一个很大的数，输出的结果对10000取模。

输入

第一行输入两个整数n,m(1 <= n,m <= 100)。表示棋盘的大小。接下来输入n行,每行m个整数e(0 <= e < 20)。

输出

对于每一组数据输出方式总数对10000取模的结果.

样例

输入

6 6
4 5 6 6 4 3
2 2 3 1 7 2
1 1 4 6 2 7
5 8 4 3 9 5
7 6 6 2 1 5
3 1 1 3 7 2

输出

3948

补充

时间限制 1 秒
内存限制 128 MB
来源 FYOJ

题解

咳咳咳，进入题解部分

老师的做法

额……
老师直接暴力
骗分过样例，暴力出奇迹！
接着直接看他的代码吧

#include <cstdio>
using namespace std;
int a[111][111],f[111][111];
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i\=1; i<=n; ++i)    
        for(int j=1; j<=m; ++j)
            scanf("%d",&a[i][j]);
    //确定一个起点，确定一个终点
    //去验证这个起点->这个终点的可行性
    //a[i][j]->a[x][y]怎么去验证（i,j）->（×,y）
    //是不是只要保证a[i][j]能不能够提供我i,j--->x,y
    //重点：（i,j）--->（x,y）的距离为 x+y-i-j 
    f[1][1]=1;
    for(int x=1; x<=n; ++x)
        for(int y=1; y<=m; ++y) //x,y终点
            for(int i=1; i<=x; ++i)
                for(int j=1; j<=y; ++j) //i,j起点 
                {
                    if(i==x && j==y) continue;
                    if(x+y-i-j<=a[i][j]) f[x][y]=(f[x][y]+f[i][j])%10000;
                }                        
    printf("%d",f[n][m]);
    return 0;    
}

测评结果 通过
分数 100
时间 52 MS
内存 668 KB
语言 C++
代码长度 475

我的做法

鹅妈妈……就记忆化搜索

#include <bits/stdc++.h>
using namespace std;
int n,m;
int a[110][110];
int b[110][110];
int dfs(int x,int y){
    if (b[x][y] >= 0){
        return b[x][y];
    }
    b[x][y] = 0;
    for (int i = 0; i <= a[x][y]; i++){
        for (int j = 0; j <= a[x][y]-i; j++){
            int X = x+i,Y = y+j;
            if (X >= 1 && X <= n && Y >= 1 && Y <= m){
                int kkksc03 = dfs(X,Y);  
                b[x][y] = (b[x][y]+kkksc03)%10000;  
            }
        }
    }
    return b[x][y];
}
int main(){
    //freopen(".in","r",stdin);
    //freopen(".out","w",stdout);
    cin >> n >> m;
    for (int i = 1; i <= n; i++){
        for (int j = 1; j <= m; j++){
            cin >> a[i][j];
        }
    }
    memset(b,-1,sizeof(b));
    b[n][m] = 1;
    int chen_zhe = dfs(1,1);
    cout << chen_zhe;
    return 0;
}

测评结果 通过
分数 100
时间 7 MS
内存 816 KB
语言 C++
代码长度 732